Apuntes: Fórmulas, ecuaciones y propiedades para operaciones algebráicas
Propiedades de Exponentes [Potenciación] |
Propiedades de los Radicales [Radicación] |
Propiedades de los Logaritmos [Logaritmación]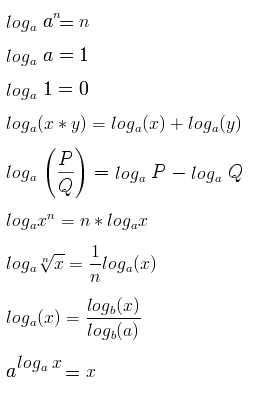 | |
Fórmulas de Productos Notables
(x + y)(x - y) = x2 - y2
(x + y)2 = x2 + 2xy + y2
(x - y)2 = x2 - 2xy + y2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x - y)3 = x3 - 3x2y + 3xy2 - y3
Fórmulas de Factorizaciones Notables
x2 - y2 = (x + y)(x - y)
x2 + 2xy + y2 = (x + y)2
x2 - 2xy + y2 = (x - y)2
x3 + 3x2y + 3xy2 + y3 = (x + y)3
x3 - 3x2y + 3xy2 - y3 = (x + y)3
x2 + bx + c = (x + d)(x + e) tal que:
d + e = b
d * e = c
Fórmula Cuadrática
Si a ‡ 0, las raices de
ax2 + bx + c = 0 son
Al término dentro de la raíz de la fórmula cuadrática se le denomina el discriminante(δ).
Si δ = 0, entonces la ecuación tiene una única solución real.
Si δ > 0, entonces la ecuación tiene 2 raices reales.
Si δ < 0, entonces la ecuación no tiene solución en el conjunto de los números reales.
Desigualdades
Si a > b y b > c, entonces a > c
Si a > b, entonces a + c > b + c
Si a > b y c > 0, entonces ac > bc
Si a > b y c < 0, entonces ac < bc
Valor Absoluto
|x| < d si y solo si
-d < x < d
|x| > d si y solo si
x > d o bien x < -d


|
Publicado por
Felipe Calvo
Ingeniero Industrial y Magíster en Estadística de la Universidad Nacional de Colombia. Consultor en políticas públicas y docente universitario. Conoce más de mi trabajo. Instagram: Felipe CalvoTwitter: @feliperspicuo |


whatshot Lo Más Popular
- Puntajes de admisión para cada carrera de la Universidad Nacional de Colombia
- Zona Interactiva: Exámenes online preparatorios para el Icfes Saber 11 y el examen de admisión de la Universidad Nacional
- Calcular promedios del examen Icfes Saber 11
- Examen de Estado ICFES - Mini Cuestionario Interactivo
- Examen de estado Icfes Saber 11: Interpretación de Resultados
bookmark_border Artículos Destacados
Pasar a la Universidad Nacional
12 Consejos para el Examen
¡Consulta tu carrera!
Consejos y Tips Examen Icfes Saber 11
¿Qué estudiar? ¿Qué repasar?
Interpretar Resultados ICFES
Calcular Promedios ICFES
Puntajes de Admisión UNAL
Estructuras y respuestas exámenes de admisión UNAL
Inscripciones ICFES y UN: paso a paso
Preguntas Frecuentes ICFES y UN
12 Consejos para el Examen
¡Consulta tu carrera!
Consejos y Tips Examen Icfes Saber 11
¿Qué estudiar? ¿Qué repasar?
Interpretar Resultados ICFES
Calcular Promedios ICFES
Puntajes de Admisión UNAL
Estructuras y respuestas exámenes de admisión UNAL
Inscripciones ICFES y UN: paso a paso
Preguntas Frecuentes ICFES y UN
forum Últimos Comentarios
person_add En Contacto
¿Deseas ponerte en contacto con nosotros?
Escribe al correo electrónico elblogdelanacho[arroba]gmail.com o contáctame a través de Instagram.


........gracias ya quedan 4 dias y estoy en el proceso de memorización de formulas ............sobre todo de identidades trigonometricas...........
perdon pero creo que en la quinta formula de productos notables te equivocaste en el signo la forma correcta es
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x - y)3 = x3 - 3x2y + 3xy2 - y3
:: Joan Gracias por el apunte. :bien:
Al término dentro de la raíz de la fórmula cuadrática se le denomina el discriminante(δ).
No entendí bien. ¿el discriminante es el 4? ¿qué es el discriminante?
Karen.
No, el 4 siempre está ahí puesto que hace arte de la fórmula cuadrática. El discriminante es la solución a lo que se encuentre dentro de la raíz, en este caso b2-4ac.
seguiras con este blog el año sig??
Publicar un comentario...
Deje su comentario empleando su ¿Qué es esto? Si utiliza servicios de Google como Gmail, Blogger, Youtube, Google Drive, entre otros, usted ya dispone de una cuenta de Google.
Haciendo click en la opción de 'Notificarme' puedes estar pendiente desde tu correo de las respuestas a tu comentario.